🏄♀️ 코딩테스트/🐍 Python
[ 백준 9370 해설 ] ( python ) 미확인 도착지
Po_tta_tt0
2022. 9. 5. 13:14
반응형
📚 미확인 도착지
문제
(취익)B100 요원, 요란한 옷차림을 한 서커스 예술가 한 쌍이 한 도시의 거리들을 이동하고 있다. 너의 임무는 그들이 어디로 가고 있는지 알아내는 것이다. 우리가 알아낸 것은 그들이 s지점에서 출발했다는 것, 그리고 목적지 후보들 중 하나가 그들의 목적지라는 것이다. 그들이 급한 상황이기 때문에 목적지까지 우회하지 않고 최단거리로 갈 것이라 확신한다. 이상이다. (취익)
어휴! (요란한 옷차림을 했을지도 모를) 듀오가 어디에도 보이지 않는다. 다행히도 당신은 후각이 개만큼 뛰어나다. 이 후각으로 그들이 g와 h 교차로 사이에 있는 도로를 지나갔다는 것을 알아냈다.
이 듀오는 대체 어디로 가고 있는 것일까?
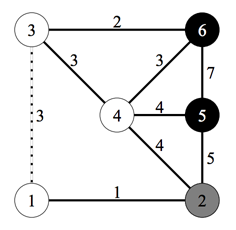
예제 입력의 두 번째 케이스를 시각화한 것이다. 이 듀오는 회색 원에서 두 검은 원 중 하나로 가고 있고 점선으로 표시된 도로에서 냄새를 맡았다. 따라서 그들은 6으로 향하고 있다.
입력
첫 번째 줄에는 테스트 케이스의 T(1 ≤ T ≤ 100)가 주어진다. 각 테스트 케이스마다
- 첫 번째 줄에 3개의 정수 n, m, t (2 ≤ n ≤ 2 000, 1 ≤ m ≤ 50 000 and 1 ≤ t ≤ 100)가 주어진다. 각각 교차로, 도로, 목적지 후보의 개수이다.
- 두 번째 줄에 3개의 정수 s, g, h (1 ≤ s, g, h ≤ n)가 주어진다. s는 예술가들의 출발지이고, g, h는 문제 설명에 나와 있다. (g ≠ h)
- 그 다음 m개의 각 줄마다 3개의 정수 a, b, d (1 ≤ a < b ≤ n and 1 ≤ d ≤ 1 000)가 주어진다. a와 b 사이에 길이 d의 양방향 도로가 있다는 뜻이다.
- 그 다음 t개의 각 줄마다 정수 x가 주어지는데, t개의 목적지 후보들을 의미한다. 이 t개의 지점들은 서로 다른 위치이며 모두 s와 같지 않다.
교차로 사이에는 도로가 많아봐야 1개이다. m개의 줄 중에서 g와 h 사이의 도로를 나타낸 것이 존재한다. 또한 이 도로는 목적지 후보들 중 적어도 1개로 향하는 최단 경로의 일부이다.
출력
테스트 케이스마다
- 입력에서 주어진 목적지 후보들 중 불가능한 경우들을 제외한 목적지들을 공백으로 분리시킨 오름차순의 정수들로 출력한다.
예제 입력 1 복사
2
5 4 2
1 2 3
1 2 6
2 3 2
3 4 4
3 5 3
5
4
6 9 2
2 3 1
1 2 1
1 3 3
2 4 4
2 5 5
3 4 3
3 6 2
4 5 4
4 6 3
5 6 7
5
6
예제 출력 1 복사
4 5
6
✍ 접근
- 문제를 잘못 읽어서 g-h를 꼭 지나야 하는 모든 곳을 출력해야 하는 줄 알고 계속 틀렸다
- 문제 : g-h를 지나는 길이 최단경로인 예상목적지가 있다
- 따라서 1. start - g - h / 2. start - h - g / 3. start - / 이렇게 세 번 다익스트라를 돌려서
결과값을 비교한 후 3 ==1 이거나 3 == 2인 결과를 출력하면 된다 - 하지만 더 쉬운 방법이 있다. 그 내용은 밑에서!
정답코드
# ✨ 입력
import sys, heapq
input = sys.stdin.readline
INF = int(1e9)
T = int(input())
# ✨ 다익스트라
def dijkstra(start):
hq = []
heapq.heappush(hq,(0,start))
dp_graph[start] = 0
while hq:
dist,node = heapq.heappop(hq)
if dist > dp_graph[node]:
continue
for n_node, n_dist in graph[node]:
dists = dist + n_dist
if dp_graph[n_node] > dists:
dp_graph[n_node] = dists
heapq.heappush(hq,(dists,n_node))
for _ in range(T):
n,m,t = map(int,input().split()) # 교차로 도로 목적지 후보 개수
s,g,h = map(int,input().split()) # 출발지, 듀오가 지나친 교차로
graph = [[] for _ in range(n+1)]
dp_graph = [INF] *(n+1)
for _ in range(m):
a,b,d = map(int,input().split())
if (a == g or a == h) and (b == g or b == h):
graph[a].append((b,d-0.01))
graph[b].append((a,d-0.01))
continue
graph[a].append((b,d))
graph[b].append((a,d))
dijkstra(s)
# ✨ 예상 목적지와 비교
res = []
for _ in range(t):
x = int(input())
if type(dp_graph[x]) == float:
res.append(x)
res = sorted(res)
print(*res)해설
입력
- 문제에서 나온 값을 입력받는다
- for문을 돌면서 graph를 만드는 부분이 중요한데,
g와 h 교차로 사이에 있는 도로의 값 - 0.01(아주 작은 값)을 빼준다.
결과적으로 dijkstra 함수를 돌면서 g와 h 교차로 사이에 있는 도로를 지나면. 그 값은 float로 저장된다는 것에 착안
준비
- graph를 그려줄 graph
- 최적값을 구할 수 있는 graph_dp
dijkstra
- 방문한 node와 dist를 이용해서 최단경로를 구해준다
예상 목적지와 비교
- 예상 목적지의 dp_graph[x] 타입이 float형일 경우. g-h혹은 h-g를 지나쳤다는 것이 되니까 res에 append해준다
⭐ 배움
- 최단거리에 꼭 지나쳐야 하는 경로를 지나쳤는지 확인할 때의 dijkstra
반응형